Optimization¶
This page mentions three ways in which code or code usage can be optimized:
- by incorporating existing subroutines from other languages into Python code (Python as a glue-language)
- by simple parallelization
- by controlling existing full-blown shell programs from within Python
Contents
Connecting programming languages with F2py¶
Python is one of the easiest languages to learn, and one of the most efficient to write. Variables need not to be declared, and can even change type within a single Python program. The batteries included strategy, and the availability of numpy, scipy and pylab allow the programmer to immediately focus on the problem at hand, without bothering with the details. Such a high-level language obviously must come at a price: speed. Although numpy and scipy already solve many of the speed issues, sometimes a problem is just to complicated to be easily integrated in the numpy and scipy framework. Also, many people, companies or institutes have a huge tradition in a particular field, resulting in a lot of code written in Fortran and C, that is fast and reliable, albeit perhaps not easy in use. It would be a tremendous waste of effort to reimplement everything in Python, probably ending up with a program which is a lot slower and less reliable than the original source code.
Luckily, Python easily interfaces with existing codes, in particular Fortran and C. This tutorial focuses on Fortran, but in fact much more tools are available for C.
An example of the interface capabilities of Python to Fortran and C is already apparent in numpy and scipy. Most of the optimization and linear algebra code are in fact wrappers around existing packages such as LAPACK and BLAS. Essentially, numpy and scipy do not re-invent the wheel. Specifically for this purpose, an f2py program is installed alongside numpy, which converts Fortran and C code to a Python library. It is important to mention that this program does not convert Fortran code to Python code (that would be slow), but instead compiles the Fortrano code to a ‘shared library’, which Python immediately understands.
An immediate disclaimer is the following: f2py only works with subroutines, and not programs. Just like any other Python function, a Fortran subroutine generally has input and output. Little change in the code is required for Python to understand what is input, and what is output. In fact, it is only necessary to add some comment statements. This implies that the Fortran code you use to generate Python modules does not need any adjustments.
FORTRAN¶
In this example, we want to ditch the FFT in favour of an explicit Fourier transform. A reason could be that one perhaps wants to oversample a Fourier transformation in a narrow passband, but the number of datapoints do not allow for much zeropadding. In that case, one could write an explicit Fourier transform in Fortran.
Click to Show/Hide FORTRAN Code
subroutine fourier(T,X,F0,DF,N,NF,FR,S1)
Cf2py intent(in) T
Cf2py intent(in) X
Cf2py intent(in) F0
Cf2py intent(in) DF
Cf2py intent(in) N
Cf2py intent(in) NF
Cf2py intent(out) FR
Cf2py intent(out) S1
implicit real*8 (a-h,o-z)
dimension T(N),X(N)
dimension FR(NF),S1(NF)
DOUBLE PRECISION TPF,F0,DF
DOUBLE PRECISION COX,SOX,TF
DOUBLE PRECISION S0,C0
DATA TWOPI/6.28318530717959D0/
TPF = F0*TWOPI
do 11 K=1,NF
C0X = 0.
S0X = 0.
do 12 I=1,N
TF = T(I)*TPF
S0 = SIN(TF)
C0 = COS(TF)
C0X = C0X + C0 * X(I)
S0X = S0X + S0 * X(I)
12 end do
S1(K) = C0X*C0X + S0X*S0X
FR(K) = TPF/TWOPI
TPF=TPF+DF*TWOPI
11 end do
RETURN
END
After writing the Fortran routine and saving it to a file fourier.f, we can run the f2py program:
$:> f2py -c fourier.f -m ffourier
The -c options tells us in which file(s) the Fortran code is located, the -m tells you the name of the Python module the Fortran code will be converted to. If the Fortran code has other *.f dependencies, you can easily compile them all in the same Python module:
$:> f2py -c *.f -m ffourier
The result should be an *.so file, which is a ‘shared library object’. This shared library can be treated as a normal Python module:
import numpy as np
import pylab as plt
import ffourier # this is our Fortran module
# generate a time series with a frequency at 0.1 Hz
times = np.linspace(0,100,1000)
signal = np.sin(2*np.pi*0.1*times)
# compute the fourier on a limited region between 0.05 and 0.15 Hz
f0,df,nf = 0.05,0.00005,2000
freqf,amplf = ffourier.fourier(times,signal,f0,df,nf)
plt.plot(freqf,amplf,'k-')
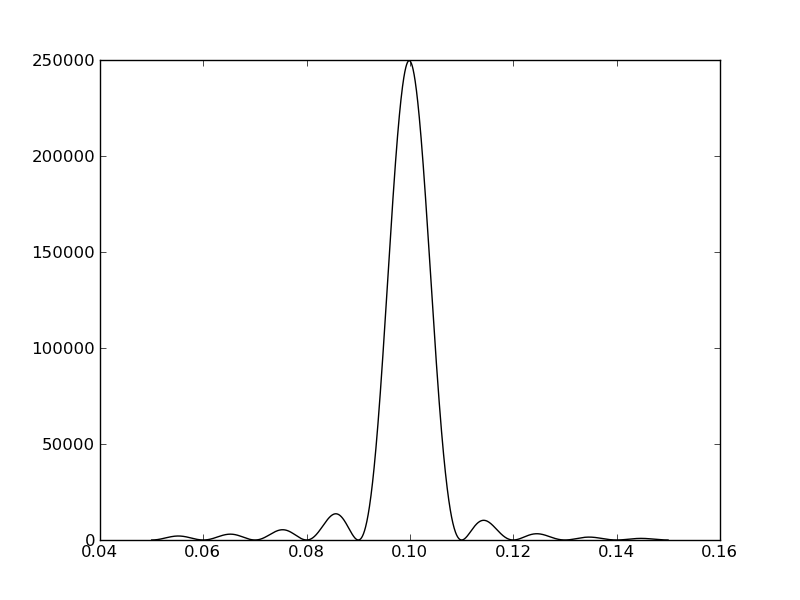
C¶
Similar things as for FORTRAN can be done with C/C++. In fact, the number of tools available for C/C++ are much more numerous (SWIG, scipy.weave, Python docs,...). However, also F2Py has (somewhat limited) functionality with C code.
Suppose we have a C implemenation of the Fortran function fourier given above.
Click to Show/Hide C Code
# include <stdio.h>
# include <math.h>
double * fourier(int n, double *t, double *x, double f0, double df, int nf, int nf2, double *fr)
{
double twopi,tf,s0,c0;
double c0x,s0x,tpf;
int k,i;
twopi = 2.0*M_PI;
tpf = f0*twopi;
for (k=0;k<nf;k++)
{
c0x = 0.0;
s0x = 0.0;
for (i=0;i<n;i++)
{
tf = t[i]*tpf;
s0 = sin(tf);
c0 = cos(tf);
c0x = c0x + c0 * x[i];
s0x = s0x + s0 * x[i];
}
fr[nf+k] = c0x*c0x + s0x*s0x;
fr[k] = tpf/twopi;
tpf = tpf + df*twopi;
}
return fr;
}
In contrast to the Fortran subroutine, we need to explicitly write a header file that explains which variables are intended as input, and which are intended as output, and save it to a file fourier.pyf:
python module cfourier
interface
subroutine fourier(n,t,x,f0,df,nf,nf2,fr) result (fr)
intent(c) fourier
intent(c)
integer intent(hide), depend(t) :: n=len(t)
double precision intent(in) :: t(n)
double precision intent(in) :: x(n)
double precision intent(in) :: f0
double precision intent(in) :: df
integer intent(in) :: nf
integer intent(hide), depend(fr) :: nf2=len(fr)
double precision intent(in,out) :: fr(nf2)
end subroutine fourier
end interface
end python module cfourier
We run the F2Py program on the header file and source code:
$:> f2py fourier.pyf fourier.c -c
And can finally use as a normal Python module. Note that the C function has a slightly different calling signature.
import numpy as np
import pylab as plt
import ffourier # this is our Fortran module
import cfourier # this is our C module
# generate a time series with a frequency at 0.1 Hz
times = np.linspace(0,100,1000)
signal = np.sin(2*np.pi*0.1*times)
# compute the fourier on a limited region between 0.05 and 0.15 Hz
f0,df,nf = 0.05,0.00005,2000
freqf,amplf = ffourier.fourier(times,signal,f0,df,nf)
freqc,amplc = cfourier.fourier(times,signal,f0,df,nf,np.zeros(2*nf)).reshape((2,-1))
plt.plot(freqf,amplf,'k-')
plt.plot(freqc,amplc,'r--')
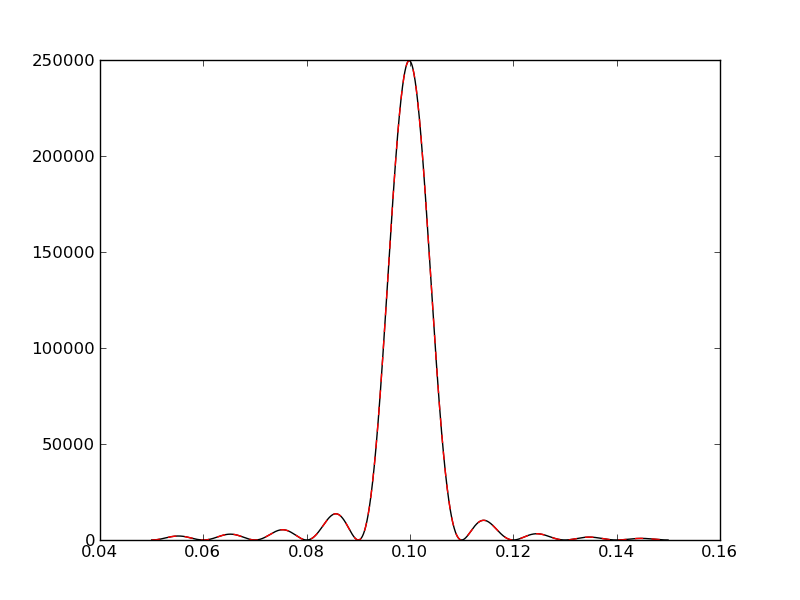
Multiprocessing¶
Usually, you want to write stuff in Fortran because it needs to be fast. Another solution to write fast code is parallelization. Better yet, how cool would it be to write Fortran code and parallelize it in Python?
The multiprocessing package was introduced as of Python 2.6. It is partially inspired on the threading package. The difference with the latter is that multiprocessing actually makes use of different cores, while threading only allows different threads on one core.
The multiprocessing package provides high-level tools for parallelization, such as exchanging objects between processes, synchronization, Pools and Queues. In the following example, we divide the Fourier computations done above over all the cores that are available on a computer. This can simply be done by dividing the domain of the Fourier transform in pieces. We need to define a function that computes one of these pieces. It is almost identical to the ffourier.fourier defined before, except that we need also to pass the power-spectrum array to fill in as a shared object (power), and we need to know which part of the Fourier transform is beeing computed (given by the starting index start).
def fourier_process(times,signal,f0,df,nf,power,start):
f1,s1 = ffourier.fourier(times,signal,f0,df,nf)
power[start:start+nf] = s1
Next, a function is need that divides the Fourier transform in the pieces, and spawns a multiprocessing.Process with the adequate arguments. Note that the number of cores available on a computer can simply be returned with the function multiprocesssing.cpu_count().
def fourier(times,signal,f0,df,nf):
nproc = multiprocessing.cpu_count()
arr = multiprocessing.Array('d',range(nf)) # shared object for the power spectrum
processes = [] # a list containing all the processes that will be spawned
for i in range(nproc):
nf_run = nf/nproc # how many frequency points need to be sampled per process
start = i*nf_run # starting index
startf = f0+start*df # starting frequency
p = multiprocessing.Process(target=fourier_process,args=(times,signal,startf,df,nf_run,arr,start))
p.start() # start the process
processes.append(p) # and add it to the list
for i in processes:
i.join() # wait until process has ended
return f0+np.arange(nf)*df,np.array(arr) # and return the results
If you don’t want to share data between process, there exist more elegant ways of solving the problem. Suppose we want to median filter several FITS images in parallel. We can then use the multiprocessing.Pool function in combination with the map function:
import os
import glob
import multiprocessing
import shutil
import pyfits
from scipy.ndimage import median_filter
# Define a function to run on files. The steps are:
# - read in FITS file
# - convolve the data in the primary HDU
# - write out the result to a new file
def smooth(filename):
print "Processing %s" % filename
hdulist = pyfits.open(filename)
hdulist[0].data = median_filter(hdulist[0].data, 15)
hdulist.writeto(filename.replace('files/', 'files_smooth/'),
clobber=True)
# Search for all FITS files
files = glob.glob('files/*.fits')
# Remove output directory if it already exists
if os.path.exists('files_smooth'):
shutil.rmtree('files_smooth')
# Create output directory
os.mkdir('files_smooth')
# Define a 'pool' of 12 processes
p = multiprocessing.Pool(processes=12)
# Run the function over all files in parallel
result = p.map(smooth, files)
Running and controlling shell programs¶
The subprocess module provides an interface to run programs (subprocess.call) and return the standard output (subprocess.check_output). One can invoke programs in the shell (shell=True), to still have access to shell features (wildcards, pipes, environment variables).
It is also possible to communicate with a program and its output while it is executed, so you don’t have to wait until it terminates. This can be used to check how a program is advancing, and maybe terminate it to restart it with different input. We give an example of some of the possibilities, by running a stupid Fortran program dummy, that writes out the numbers from 0 to 20 and their squared value, at a rate of 1 number per second.
PROGRAM DUMMY
real match,number
integer i
number = 0.0
do 10,i=0,20
write(*,*) number,'**2 =',number**2
call sleep(1)
number = number+1.0
10 CONTINUE
end
Which can be compiled to the default a.out by simply running:
$:> gfortran dummy.f
or something similar.
Now the idea is to write a small Python wrapper around it, that reads in the input and kills it when it reaches a certain number. For fun, we will also stop the program for a few seconds when it reaches the number 5, to continue afterwards again. Finally, we check if the number we gave was reached: if the returncode is 0, it exited normally (and we did not reach the number), if the returncode is nonzero, it was killed, and the number was reached.
The modules we need are of course subprocess to launch and control the Fortran program, signal to stop, continue and kill a process, sys to get user input from the terminal, and time let the program sleep between the stop and continue signal.
import subprocess
import signal
import time
import sys
Next, we need some kind of iterator that iterates over the output generated from the Fortran program, waits until the next output is received, and ends after the output stream is closed. This is simply done with:
def line_at_a_time(fileobj):
while True:
line = fileobj.readline()
if not line:
return
yield line
Finally, we write the main part of the program. It will get a the number to stop the program at from the command line via the sys.argv variable, start the Fortran program, catching its standard output to a pipe:
match_number = float(sys.argv[1])
p1 = subprocess.Popen('./a.out',stdout=subprocess.PIPE)
The return value p1 is a Popen object. For a full description, see the docs. It has an attribute called stdout, which is a file-like object than can be given to the read function defined above. We will extract the current number from the output of the Fortran program, and check if it matches The user-given variable match_number. If it does, we send a kill signal SIGKILL to the process, which will kill it. If the number reaches 5, we sill stop it, wait for 5 seconds and continue again. Else, the program will just report the last line it received from the Fortran program:
for line in line_at_a_time(p1.stdout):
check = float(line.split('*')[0])
if check==match_number:
print('I got: "{0}"; and it is a match! Killing program now...'.format(line.strip()))
p1.send_signal(signal.SIGKILL) # equivalent to os.kill(p1.pid,signal.SIGKILL)
elif check==5.:
print('I got: "{0}"; that is a nice number, I will just wait here for a moment...'.format(line.strip()))
p1.send_signal(signal.SIGSTOP)
time.sleep(5)
print('... waited long enough, continuing...')
p1.send_signal(signal.SIGCONT)
else:
print('I got: "{0}"; but we are not yet at {1}'.format(line.strip(),match_number))
And finally, we make sure the Fortran program is finished, and ask for its return code:
retcode = p1.wait()
if retcode==0:
print("The program exited normally (return code: {0})".format(retcode))
else:
print("The program terminated prematurely (return code: {0})".format(retcode))
After saving the code to the file program_control_shell.py, we can run it with:
$:> python program_control_shell.py 10
I got: "0.0000000 **2 = 0.0000000"; but we are not yet at 10.0
I got: "1.0000000 **2 = 1.0000000"; but we are not yet at 10.0
I got: "2.0000000 **2 = 4.0000000"; but we are not yet at 10.0
I got: "3.0000000 **2 = 9.0000000"; but we are not yet at 10.0
I got: "4.0000000 **2 = 16.000000"; but we are not yet at 10.0
I got: "5.0000000 **2 = 25.000000"; that is a nice number, I will just wait here for a moment...
... waited long enough, continuing...
I got: "6.0000000 **2 = 36.000000"; but we are not yet at 10.0
I got: "7.0000000 **2 = 49.000000"; but we are not yet at 10.0
I got: "8.0000000 **2 = 64.000000"; but we are not yet at 10.0
I got: "9.0000000 **2 = 81.000000"; but we are not yet at 10.0
I got: "10.000000 **2 = 100.00000"; and it is a match! Killing program now...
The program terminated prematurely (return code: -9)
or:
$:> python program_control_shell.py 25
I got: "0.0000000 **2 = 0.0000000"; but we are not yet at 25.0
I got: "1.0000000 **2 = 1.0000000"; but we are not yet at 25.0
I got: "2.0000000 **2 = 4.0000000"; but we are not yet at 25.0
I got: "3.0000000 **2 = 9.0000000"; but we are not yet at 25.0
I got: "4.0000000 **2 = 16.000000"; but we are not yet at 25.0
I got: "5.0000000 **2 = 25.000000"; that is a nice number, I will just wait here for a moment...
... waited long enough, continuing...
I got: "6.0000000 **2 = 36.000000"; but we are not yet at 25.0
I got: "7.0000000 **2 = 49.000000"; but we are not yet at 25.0
I got: "8.0000000 **2 = 64.000000"; but we are not yet at 25.0
I got: "9.0000000 **2 = 81.000000"; but we are not yet at 25.0
I got: "10.000000 **2 = 100.00000"; but we are not yet at 25.0
I got: "11.000000 **2 = 121.00000"; but we are not yet at 25.0
I got: "12.000000 **2 = 144.00000"; but we are not yet at 25.0
I got: "13.000000 **2 = 169.00000"; but we are not yet at 25.0
I got: "14.000000 **2 = 196.00000"; but we are not yet at 25.0
I got: "15.000000 **2 = 225.00000"; but we are not yet at 25.0
I got: "16.000000 **2 = 256.00000"; but we are not yet at 25.0
I got: "17.000000 **2 = 289.00000"; but we are not yet at 25.0
I got: "18.000000 **2 = 324.00000"; but we are not yet at 25.0
I got: "19.000000 **2 = 361.00000"; but we are not yet at 25.0
I got: "20.000000 **2 = 400.00000"; but we are not yet at 25.0
The program exited normally (return code: 0)
