Introduction

We are given:

• observational data
• a model with a set of fit parameters

Goal: Minimize squared difference between some model and some given data.

Linear vs. non-linear models

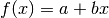• (straight line)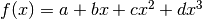
• 
• 

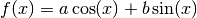
If the optimization problem is a least-squares problem, fitting linear models can be done analytically using linear algebra (matrices)! However, many interesting astrophysical problems are not linear! Examples for non-linear models are:

• 
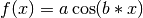
• fitting emission/absorption features in a spectrum
• fitting light profiles of galaxies (morphology)

For nonlinear models or linear models without least-squares formulation, there is usually no analytic solution and the likelihood may also be multimodal. In this case, we need an optimization algorithm in order to fit the model parameters.

First Idea: Brute-force grids

Try brute-force all combinations of fit parameters and find the optimum of the objective function.

Let’s create some toy data:

import numpy
import matplotlib.pyplot as plt

# Create 1D Gaussian data.
numpy.random.seed(1)  # set random seed
# Draw 10 values from unit Gaussian.
Data = numpy.random.normal(0.0, 1.0, 10)

Our model is a straight line with true parameters offset a = 0.0 and slope b = 0.0. Fit for a and b using a brute-force grid:

# Range of parameter a.
a_min = -2.5
a_max =  2.5
# Range of parameter b.
b_min = -1.0
b_max =  1.0
# Number of steps of grid.
steps = 51
# Allocate grid as matrix.
grid  = numpy.zeros([steps,steps])
# Try all parameter combinations.
for s1 in range(steps):
    for s2 in range(steps):
        # Current parameter combination.
        a = a_min + (a_max - a_min)*float(s1)/float(steps-1)
        b = b_min + (b_max - b_min)*float(s2)/float(steps-1)

        # Evaluate chi-squared.
        for n in range(len(Data)):
            # Use index n as pseudo-position
            residual = (Data[n] - a - n * b)
            chi2 = residual * residual
        grid[steps - 1 - s2, s1] = chi2

plt.figure(1, figsize=(8,3))
mini  = numpy.min(grid)  # minimal value of chi2
image = plt.imshow(grid, vmin=mini, vmax=mini+20.0,
                         extent=[a_min,a_max,b_min,b_max])
plt.colorbar(image)
plt.xlabel(r'$a$', fontsize=24)
plt.ylabel(r'$b$', fontsize=24)
plt.savefig('example-chi2-manifold.png')
plt.show()

Here is what the resulting 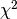-manifold looks like:

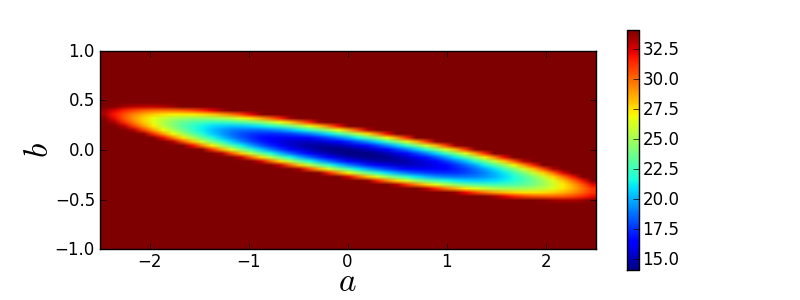
Brute-force grids may seem naive but this method is the first to consider! Note that brute-force grids quickly become computationally infeasible for more than 1 or 2 fit parameters. Computation times increase exponentially, so more intelligent methods are needed.